精密
离心机主要用于线加速度计等惯性仪表的校准 [1-2] 。静态半径是向心加速度的重要组成部分,其 和检测 高精度测量关系到精密
离心机输出加速度值的准确度和 不确定度,进而影响加速度计的校准和检测精度 精 密
离心机静态半径的测量不确定度**少要比精密离心机输出加速度的测量不确定度高 1 倍甚**更高,对于加速 度相对标准不确定度为 10
- 5 或 10
- 6 量级的精密离心机, 其对静态半径测量方法、测量系统以及精密离心机自身 的整体性能都提出了极高要求。目前G内外主要有 2 种静态半径测量方法。一是采用精密量块和基准环或激光自准直仪等进行直接测
[4-6]
量 。该方法受离心机主轴回转误差和加速度计质心不确定性影响较大,且测量环节多,测量精度不高,一般
只用于低精度的精密离心机静态半径测量。
[7]
反算法 测量静态半径是以重力场下的某个加速度值( 一般取 1g) 为基准,调整精密离心机转速使待测加速度计输出值等于该基准值,通过修正的加速度载荷公式来反算该状态下的工作半径,以此作为精密离心机的基准半径,其他状态的工作半径等于该基准半径加上相应的离心机转盘或大臂的径向动态变化量。文献[8]提供的静态半径反算法只考虑向心加速度,适用于一般精度或低精度的精密离心机; 文献[9]提出的静态半径反算法测量精度有所提高,但没有考虑加速度计制造及安装夹具带来的俯仰失准角对静态半径的影响,而且受加速度计自身、加速度模型方程以及测量仪器的系统偏差影响较大,也不能用于高精度精密离心机的静态半径测量。此外,采用测量不确定度来定量评价测量结果的精度在G内外正成为一种趋
[10-14],
势 然而精密离心机静态半径测量不确定度评定方面的工作G内外没有公开的文献报道,G内仅有 2 篇文献作
[5-6]
了简要的叙述和说明 。由于高精度精密离心机及其静
态半径测量很难采用更高精度的仪器或设备来检定、校核其精度,科学、合理的测量不确定度评定模型及评定方法
就变得非常重要。
本文提出一种改进的反算法,使之能够应用于 10
- 5 以下量级的高精度精密离心机静态半径测量,构建测量系统及不确定度评定模型,并在自研的 10
- 5 量级精密离
心机静态半径测量中得到了较好应用。
2 静态半径测量反算法
2. 1 测量原理
不同精度等级的精密离心机对静态半径测量精度要求不同,表 1 给出了不同精度的精密离心机对应的工作半径测量精度要求。工作半径等于静态半径与动态半径之和,故静态半径的测量精度还要高于表 1 中数值。对于高精度精密离心机,静态半径测量精度要求极高,其测量过程中考虑的影响因素增多,这些需要考虑的因素在
下文中进行分析。
[4]
表 1 精密离心机等级分类
Table 1 Classification of precision centrifuge

|
序号 |
精密离心机 |
精密离心机加速度 |
工作半径测量不 |
|
准确度等级准 |
测量不确定度 |
确定度要求 |
|
|
|
|
|
|
|
|
1 |
0. 1 级 |
10 - 3 |
5 × 10 - 4 |
|
2 |
0. 01 级 |
10 - 4 |
5 × 10 - 5 |
|
3 |
0. 001 级 |
10 - 5 |
7 × 10 - 6 |
|
4 |
0. 000 1 级 |
10 - 6 |
7 × 10 - 7 |

采用待测加速度计输出值来反算精密离心机静态半径的原理如图 1 所示。静态半径定义为主轴回转轴线到待测加速度计有效质量中心的距离。待测加速度计输入轴与精密离心机工作半径方向重合时,加速度计感受到的加速度含有向心加速度,而向心加速度又是静态半径的函数,故加速度计输出值中含有静态半径的信息。结合加速度计在重力场下校准得到的一阶静态模型方程以及其他测量分量,按照已确定的精密离心机输出到加速度计输入轴上的加速度数学模型即可反解出此状态的静态半径值,精密离心机在工作状态的半径等于该静态半径值与转盘或大臂的径向动态变化量之代数和。
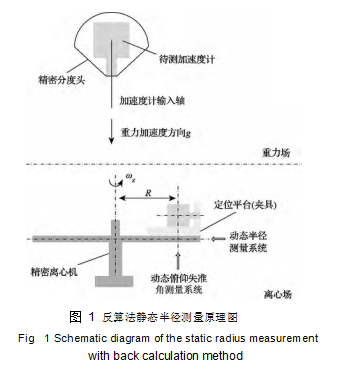
上述反算法测量静态半径的具体步骤如下:
第 1 步: 使用**重力仪测量当地重力加速度值,并用精密分度头等专业仪表使加速度计工作轴向与重力加
速度方向成不同的角度,读取加速度计在 0 ~ 1g 加速度输入下的电压或电流输出值,拟合出加速度计在重力场下的零次项系数和标度因数,标定出加速度计的一次静态模型方程;
第 2 步: 将待测加速度计安装到精密离心机的定位平台或夹具上,调整加速度计姿态使加速度计输入轴尽量与精密离心机工作半径方向重合。
第 3 步: 驱动精密离心机转动,使待测加速度计
输出电压或电流等于 U
g ( U
g 对应的加速度计输入值记为 a
g ,通常基准 a
g 约为 1 g 或小于 1 g ) 时,稳定转速,此时的转速记为 ω
g 。对于较高精度的精密离心机,此状态下加速度计输入轴上感知的加速度除了向
|
心加速度,还包括重力加速度以及科里奥利加速度 |
|
等,根据加速度载荷简化公式,有: |
|
|
|
|
|
|
|
|
ag = ω2g R + λg g ± 2ωg ωε Rsin θ |
( 1) |
|
为了便于测量,式( 1) 可以进一步转化为: |
|
|
ag = ω2g R + ( λ + λg ) g ± 2ωg ωε Rsin θ |
( 2) |
|
式中: R 为精密离心机在加速度 ag 下的基准半径,即静 |
|
态半径; λg 为角速度等于 ωg 时的俯仰失准角,rad,包括 |
|
动态俯仰失准角 λg 和静态俯仰失准角 λ; ωε |
为地球自 |
|
转角速度,rad / s; θ 为精密离心机所在之地的地球纬度。 |
|
对于北半球G家,精密离心机逆时针方向旋转时式( 1) 、 |
|
( 2) 中“± ”号取“+ ”。 |
|
|
|
|
通过式( 1) 即可反解出静态半径为: |
|
|
|
ag - λg g |
|
ag - ( λ + λg ) g |
( 3) |
|
R = |
|
= |
|
|
|
|
ω2g ± 2ωg ωε sin θ |
|
ω2g ± 2ωg ωε sin θ |
|
|
|
|
|
|
|
|
式中: |
|
|
|
|
ag = Ug / k1 - k0 |
|
|
( 4) |
|
|
|
|
|
|
式中: k0 为待测加速度计的偏值,g 或 m / s2 ; k1 为待测加 |
|
|
|
速度计的标度因素,V / g 或 A / g。 |
|
|
|
|
|
联合俯仰失准角和旋转角速度测量结果,即可得到 |
|
|
|
静态半径值。式( 1) 可看出,俯仰失准角 λg 应该包括加 |
|
|
|
速度计输入轴和安装夹具带来的失准角偏差,然而实际 |
|
|
|
采用电子水平仪测量得到的俯仰失准角是定位平台或离 |
|
|
|
心机大臂相对于地球表面的角度。即使采用其他测量装 |
|
|
|
置也很难直接准确测量得到加速度计输入轴相对于地表 |
|
|
|
的俯仰失准角。粗略计算,1″的俯仰失准角偏差将导致 |
|
|
|
静态半径 5 × 10 - 6 的相对误差,而实际加速度计及安装夹 |
|
|
|
具的俯仰失准角不止 1″。因此如何补偿不可测的俯仰失 |
|
准角成为制约上述静态半径测量方法在高精度精密离心 |
|
|
|
机上应用的关键。 |
|
|
|
|
|
|
|
|
|
此外,待测加速度计自身分辨率以及各测量仪器 |
|
|
|
的误差将通过式 ( 3 ) 的间接测量关系影响静态半径 |
|
|
|
|
|
|
|
反算精度。精密离心机输出加速度因素考虑不全面 |
|
|
|
也会导致加速度模型式 ( 1 ) 与加速度计实际输入的 |
|
值存在偏差,进而影响静态半径测量准确度。一般精 |
|
密离心机的精度都是高于待标定加速度计的精度 1 |
|
或 2 个量级,而静态半径测量精度又必须高于精密离 |
|
心机的精度。表面上看,采用低精度的待测加速度计 |
|
|
|
来反算高精度的静态半径是矛盾的。实际上反算法 |
|
|
|
测量静态半径只利用了重力场下的加速度计输入输 |
|
出特性。重复性精度方面,待测加速度计在重力场下 |
|
已校准得到的一次静态模型以及精密离心机主轴转 |
|
速的重复性精度可以做到很高,能够满足静态半径测 |
|
量重复性精度要求。系统误差方面,上述反算法受加 |
|
速度计自身和加速度模型方程式 ( 4 ) 以及测量仪器 |
的系统偏差影响较大。
|
2. 2 |
反算法改进 |
|
|
|
|
|
|
|
|
传统的静态半径反算法是将待测加速度计安装到精 |
|
|
|
密离心机上,调整好加速度计输入轴姿态尽量与精密离 |
|
心机工作半径方向重合后,直接驱动精密离心机旋转,记 |
|
录加速度计输出值 Ug 和对应的转速 ωg ,其中 Ug 对应的 |
|
加速度计输入值为 ag ,通常 ag 约为 1g 或小于 1g。本文 |
|
提出的静态半径反算法是在调整好待测加速度计输入轴 |
|
尽量与精密离心机工作半径方向重合后,进行以下 2 次 |
|
反算: |
|
|
|
|
|
|
|
|
|
|
|
|
|
shou先,不启动精密离心机旋转,直接读出此时待测加 |
|
速度计的输出电压或电流值,记为 U0 。由于此状态精密 |
|
离心机转速为零,加速度计输入轴感知到的加速度只有 |
|
俯仰失准角作用下的重力加速度,即: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 5) |
|
|
a0 = gλ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
式中: a0 为不启动离心机时的待测加速度计输入值; λ 为 |
|
加速度计输入轴相对于地表的静态俯仰失准角,rad。 |
|
一般电子水平仪测量得到的是定位平台或离心机大 |
|
|
|
臂相对于地表的俯仰失准角,故将 λ 分为 2 个角度之和 |
|
|
|
的形式,即: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 = g( λ0 + λ1 ) |
|
|
|
|
|
( 6) |
|
|
|
|
|
|
|
|
|
|
|
式中: λ0 为可测量的定位平台或大臂相对于地表的静态 |
|
|
|
俯仰失准角,rad。λ1 为不可测的或测不准的加速度计静 |
|
|
|
态俯仰失准角,rad。 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其次,启动精密离心机旋转,使待测加速度计输出电 |
|
|
|
压或电流为基准值 Ug ,稳定转速,读出此时的精密离心 |
|
|
|
机转速 ωg 。有: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ag = ω2g R + ( λ0 |
+ λ1 + |
|
λg ) g ± 2ωg ωε Rsin θ |
( 7) |
|
|
式中: λg 为 ωg 转速下的动态俯仰失准角,rad。 |
|
|
|
|
|
|
|
式( 6) 与( 7) 相减,并利用重力场下已标校好的待测 |
|
|
|
加速度计标度因数 k1 ,有: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ag - a0 - |
λg g |
( Ug - U0 ) / k1 - λg g |
|
|
|
R = |
|
|
|
|
( 8) |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
± 2ωg ωε sin θ |
|
|
|
|
|
|
|
ωg |
|
|
ωg ± 2ωg ωε sin θ |
|
|
|
如果调整待测加速度计在精密离心机定位平台上的 |
|
姿态后静态俯仰失准角和方位失准角仍然较大,其量级 |
|
影响了静态半径的测量精度,则必须补偿二者对静态半 |
|
径的影响,其影响规律按式( 9) 进行补偿: |
|
|
|
R = |
|
|
|
( Ug - U0 ) / k1 |
- λg g |
|
( 9) |
|
|
|
( |
|
2 |
) |
cos λ0 cos λ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ωg ± 2ωg ωε sin θ |
|
|
|
|
式中: λ2 为可测量的方位失准角,即加速度计安装平台 |
|
在上平面内相对于离心机半径方向的偏角,rad。 |
|
|
|
式( 8 ) 或 ( 9 ) 是本文提出的静态半径计算模型, |
|
该测量方法补偿了不可测的加速度计输入轴和夹具 |
|
安装俯仰失准角对静态半径的影响; 而且通过两次加 |
|
速度计的输入加速度值相减,加速度计自身、精密离 |
|
心机加速度模型、测量仪器中的系统误差以及加速度 |
|
计偏值 k0 被抵消,进一步提高了测量准确度。此外,与原有反算法相比,该测量方法不需要对静态俯仰失准角进行测量,减小了测量误差源。改进后的静态半径反算法测量过程如图 2 所示。 |
|
|
|
|

可编程精密电源采用 Agilent B2900 A 型,为待测加速度计提供高精度 ± 15 V 电压,加速度计输出电压或电流利用 KEITHLE2002 型八位半数字万用表并经
GPIB 接口传输到 PXI 机箱。角速度测量系统主要由圆光栅编码器与频率计组成,圆光栅编码器反馈信号通过频率计计算得到精密离心机的转速,自研的精密离心机实际角速度相对不确定度可控制到 10
- 7 ~
10
- 8 量级。动态俯仰失准角是通过电容测微仪测量精密离心机转盘边沿的上下摆动位移量来间接测量,利用光栅输出的 Z 脉冲对测点定位,消除转盘表面形状误差。由水银集流环传输到 PXI 机箱进行信号展宽、滤波等调理。电容测微仪为德G米铱公司的 CS 系列,采用定位测量,其测量不确定度可以控制到亚微米量级。
4 测量不确定度评定模型
由于误差评估固有的缺陷,例如不可量化、误差定义
[15]
与实际评定不符 。越来越多的学者采用测量不确定度来评价测量结果的精度。高精度精密离心机对静态半径测量精度要求非常高,因此,科学合理的测量不确定度
评定变得异常重要。
上述改进的静态半径测量模型中,静态半径 R 通过间接测量得到,其测量误差源主要来自于加速度基准 a
g ( 或 U
g ) 、a
0 ( 或 U
0 ) 、动态俯仰失准角 λ
g 、旋转角速度 ω
g 4 个分量。测量模型中的其余常量只要取足够的有效位数,引入的不确定度可忽略不计。需要注意的是 U
g 和 U
0 ( 即 a
g 和 a
0 ) 是同一加速度计的输出值,二者明显相关。基于测量不确定度传递公
[15]
式 ,通过推导、简化,静态半径测量不确定度传递模型为:
u
r ( R) ≈

|
2 |
( ω ) + |
g2 |
2 |
( |
λ ) |
2 |
( a ) |
|
a02 |
2 |
( a ) |
2ra0 |
u' ( a ) u' ( a ) |
|
4 u |
|
u |
+ u |
+ |
|
u |
- |
|
|
|
|
|
|
|
r |
g |
a2g |
|
|
g |
r |
g |
|
a2g |
r |
0 |
|
ag |
r gr 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 10) |
式中: u
r ( R) 是静态半径 R 的相对标准不确定度; u
r ( ω
g ) 是角速度 ω
g 的相对标准不确定度; u
r ( a
g ) 是加速度 a
g
的相对标准不确定度; u( λ
g ) 是动态俯仰失准角 λ
g 的
标准不确定度,rad; u
r ( a
0 ) 是加速度 a
0 的相对标准不确定度; u
'r ( a
g ) 是 a
g 的由系统效应引入的相对标准不确定度; u
'r ( a
0 ) 是 a
0 的由系统效应引入的相对标准不确定度; r 是 a
0 与 a
g 的相关系数。
一般 a
g ≈g,a
g 和 a
0 不在同一数量级,且 a
g > > a
0 ,其相关系数较小可以不考虑,而且 u
r ( a
0 ) 的传递系数很小,则静态半径测量不确定度传递模型可简化为:
u
r ( R) ≈ 4u
2r ( ω
g ) + u
2 ( λ
g ) + u
2r ( a
g ) ( 11) 需要说明的是,式( 11 ) 的计算结果准确性不比式 ( 10 ) 差,这是由模型本身的特征决定的,为了简化评

定复杂度,本文采用式 ( 11 ) 作为静态半径测量不确定度的传递模型,其不确定度值由加速度值 a
g 、动态俯仰失准角 λ
g 以及旋转角速度 ω
g 3 个分量决定。5 10
- 5 量级精密离心机静态半径实测
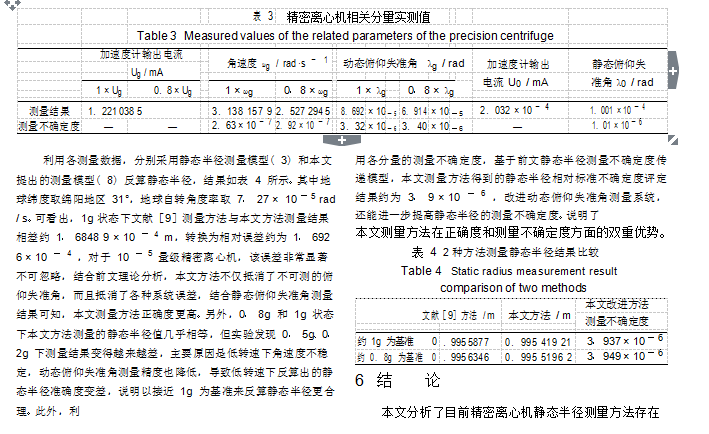
图 4 所示是利用所提方法对研制的加速度相对标准不确定度为 10
- 5 量级的精密离心机静态半径进行测量的实物图。安装就绪后先旋转离心机到高速借助离心力将螺栓紧固。实际应用时加速度计输入轴指向主轴和相反方向 2 种状态的静态半径不相等,可以取两者的平均作为静态半径值,亦或分开测量。


的问题,提出一种改进的静态半径测量方法。推导出该测
量方法新的数学模型以及对应的测量不确定度传递模型。搭建了测量系统,对研制的 10
- 5 量级精密离心机静态半径进行了实测。相同条件下,本文测量方法与基于文献[9]的测量结果相差 10
- 4 量级,该偏差对 10
- 5 和 10
- 6 量级的精密离心机影响严重,不可忽视。本文方法的静态半径相对标准不确定度评定结果约为 3. 9 × 10
- 6 。理论分析和实测结果说明了本文测量方法在正确度和不确定度两方面具
有的双重优势。
反算法测量的是加速度计质心到主轴回转轴线的距离,准确度远高于基于精密量块等仪器的直接测量方法,而且本文提出的反算测量方法补偿了不可测的俯仰失准
角、加速度模型以及测量仪器的系统误差对静态半径测量精度的影响,测量准确度得到了较大提高。本文提供的测量方法及不确定度评定模型可以为 10
- 5 或 10
- 6 量
级的高精度精密离心机研制提供一定的技术支撑。




